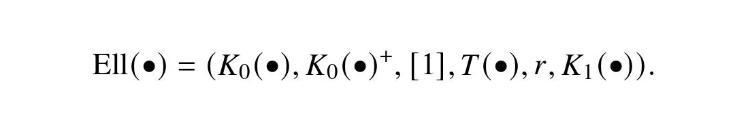Structure and classification of C*-algebras

C*-algebras are the basic structures of operator algebra theory and noncommutative geometry. Abstractly they are defined as a class of complex Banach algebras endowed with an involution operation. They can be thought of as noncommutative locally compact spaces and exhibit a rich structure, playing a pivotal role in various branches of mathematics and mathematical physics, providing a rigorous framework for quantum mechanics and non-commutative geometry. Moreover, their influence extends to other areas like index theory, representation theory, and the study of dynamical systems.
Their theory has seen a tremendous development over the past 50 years with many highlights such as the classification of injective factors in the 1970s, subfactor theory in the 1980s and 90s and the recent comprehensive results in the classification of simple nuclear C*-algebras using K-theory and other invariants.
Many questions about the structure and classification of C*-algebras remain open, for instance in relation to dynamical systems and related to the problem of finding finer invariants to classify further classes of algebras, including non-simple ones.