Student news
Published: 3 February 2015
Student news
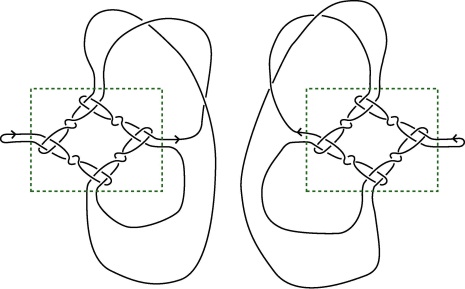
A student of Liam Watson's, Joseph MacColl (now in 4th year honours), recently posted “Rotors in Khovanov homology” – the results of his Carnegie Vacation Scholarship project – to the arXiv.
Joseph's work studies an operation on links that produces pairs of distinct links (called rotants) that cannot be detected by the Jones polynomial. His work shows that, in certain cases, Khovanov homology is sensitive to this change. This is a new result: despite the homology's relationship to the Jones polynomial, the behaviour of Khovanov homology for rotant pairs was not known prior to Joseph's discovery of pair of links pictured below.
First published: 3 February 2015
<< February 15

